1.はじめに
これまで幾つかの記事で状態遷移の集計方法の検討、検討内容に基づいた集計結果を公開を行い、次いでまず状態遷移パターンの出現確率に基づくエントロピーを計算した後、マルコフ過程と見做した場合のエントロピーの計算を行い、結果を報告してきました。
一方、集計結果に基づく分析としては、まず状態遷移パターンの多様性に基づき、従来和音の出現頻度に基づいて実施してきた各種の分析(クラスタ分析・主成分分析)を適用してマーラーの交響曲間・マーラーと他の作曲家の作品間の比較・分類を行った結果を記事:後期マーラーの「挑戦」?:MIDIファイルを入力とした分析:状態遷移パターンの多様性に注目した予備分析において報告しています。
そこで本記事では、和音の状態遷移の系列をマルコフ過程と見做した場合のエントロピーの計算結果を用いて、マーラーの交響曲間の比較・分類を行った結果を報告します。その際、比較対照のために、パターン数/系列長の比率の計算結果を用いた分析も並行して実施しました。パターン数/系列長の比率の計算結果を用いた分析は上記の通り既に実施・報告済ですが、ここではエントロピーの計算結果に基づく分析との比較対照を目的として、エントロピーの計算に用いたのと同一の抽出条件を用いて作成した和音パターンの遷移系列についてパターン数/系列長の比率の計算を行い、その結果に基づいて、エントロピーの計算結果に対してと同じ分析を実施したので、その結果も併せて報告します。(後述のパターン数/系列長の比率に基づく分析結果と、記事:後期マーラーの「挑戦」?:MIDIファイルを入力とした分析:状態遷移パターンの多様性に注目した予備分析の分析結果を比較して頂ければわかる通り、結果的には両者に大きな違いはなく、特に後期作品(「大地の歌」、第9、第10交響曲)が1グループを形成するという点は共通であることが確認できたことから、予備分析でも確認できた傾向は和音パターンの系列の抽出条件の細かい違いには依らず、比較的安定した特徴であると言えると思います。)
2.分析条件
- 入力データ:記事:MIDIファイルを入力とした分析:マルコフ過程としてのエントロピー計算結果で報告した、以下の条件で抽出した和音の系列をマルコフ過程と見做した場合のエントロピーの計算結果およびパターン数/系列長の比率の計算結果を用いました。
- エントロピー
- 各拍(A)/単音・重音は対象外(cdnz3)/移置を区別・転回は長短三和音のみ区別(tonic)。二重マルコフ・エントロピーは計算結果には含めてありますが、ほとんどの場合で0だったため、分析の入力には含めていません。
- 単純マルコフ・エントロピー(markov3_tonic1)
- 深さ0~4の状態遷移パターン・エントロピー(frq3_tonic0~4)
- 各拍(A)/単音・重音を含む(cdnz)/移置を区別・転回は長短三和音のみ区別(tonic).。二重マルコフ・エントロピーは計算結果には含めてありますが、ほとんどの場合で0だったため、分析の入力には含めていません。
- 単純マルコフ・エントロピー(markov_tonic1)
- 深さ0~4の状態遷移パターン・エントロピー(frq_tonic0~4)
- 各拍(A)/単音・重音は対象外(cdnz3)/移置・転回を区別せず(pcl)
- 単純マルコフ・エントロピー(markov3_pcl1)
- 二重マルコフ・エントロピー(markov3_pcl2)
- 深さ0~4の状態遷移パターン・エントロピー(frq_pcl0~5)
- パターン数/系列長比
- 各拍(A)/単音・重音は対象外(cdnz3)/移置を区別・転回は長短三和音のみ区別(tonic)。
- 深さ0~4のパターン数/系列長比(3_tonic0~4)
- 各拍(A)/単音・重音を含む(cdnz)/移置を区別・転回は長短三和音のみ区別(tonic).。
- 深さ0~4のパターン数/系列長比(tonic0~4)
- 各拍(A)/単音・重音は対象外(cdnz3)/移置・転回を区別せず(pcl)
- 深さ0~5のパターン数/系列長比(pcl_d0~5)
- 分析手法:前回の状態遷移パターンの出現頻度を用いた分析と同様に、階層的クラスタ分析、非階層的クラスタ分析、主成分分析を行いました。階層的クラスタ分析としては、今回はcomplete法とward法の2種類、非階層クラスタ分析はk-means法を用い、Gap統計量に基づいてクラスタ数を指定しました。主成分分析に際しては、今回対象とする特徴量は全て同じ種類ですが、状態遷移の深さが増すと増大する性質を持つため、標準化を行わないと深さの大きいパターンの寄与が大きくなってしまうことが予め予想されたため、標準化を行うモードで分析を行いました。分析はR言語のバージョン 4.3.1をR Studio上で利用して実施しました。
- 分析対象のデータ:今回はマーラーの交響曲のみ(第1~10交響曲、大地の歌(m1~10, erde):括弧内は以下に示す分析結果におけるラベルを表します。)を対象としました。集計・分析は基本的には曲単位で行いました。
3.分析結果
3.1.エントロピーに基づく分析の結果
(A)クラスタ―分析
以下に示す通り、complete法、ward法とも同じ分類結果を返しており、更にk-means法での3クラスタへの分割も階層クラスタ―分析の枝の分岐(上位の2つ)に対応しており、分類は安定しているものと考えられます。
階層クラスタ―分析:complete法
階層クラスタ―分析:ward法
非階層クラスタ―分析:k-means法
クラスタ数はGap統計のシミュレーション結果に基づき決定
- 第1グループ:第1,第4交響曲
- 第2グループ:第2,3,5,6,7,8交響曲
- 第3グループ:大地の歌、第9,10交響曲
1 2 3
symA 2 0 2:初期(第1~4交響曲)
symB 0 0 3:中期(第5~7交響曲)
symC 0 0 1:第8交響曲
symD 0 3 0:後期(大地の歌、第9,10交響曲)
m1 m2 m3 m4 m5 m6 m7 m8 erde m9 m10
1 3 3 1 3 3 3 3 2 2 2
(B)主成分分析
主成分分析のサマリーを確認すると、第3主成分までで累積がほぼ97%であり、それ以下の成分の寄与は実質的にほとんどないことから、第1~3主成分までの結果を取得していますが、全体の2/3が第1主成分、3割弱が第2主成分で残りは数%に過ぎないので、以下では第1、第2主成分のみに絞って見ていくことにします。
PC1 PC2 PC3 PC4 PC5
Standard deviation 3.6140 2.3668 0.85460 0.55164 0.47722
Proportion of Variance 0.6531 0.2801 0.03652 0.01522 0.01139
Cumulative Proportion 0.6531 0.9331 0.96965 0.98487 0.99626

2種のプロットを見ると、クラスター分析で分割された、第1,4交響曲、後期作品(「大地の歌」、第9,10交響曲)とそれ以外という3つのグループを確認することができます。そこで第1主成分・第2主成分それぞれについて、各グループの特徴を確認していくことにします。
ggbiplotによる第1・2主成分軸でのプロット
第1主成分については、第1、第4交響曲がマイナス(-)、後期(「大地の歌」、第9、第10交響曲)が中立(0)、それ以外がプラス(+)という傾向にあると言って良いでしょう。負荷を確認すると、全ての成分がプラスのときにプラスであることから、相対的にエントロピーが大きいかどうかによる分類と考えることができそうです。更に負荷を細かくみると、状態遷移パターンのエントロピーについては、深さが浅い場合の得点に寄与が小さく、深さが深くなった時に得点が高くなる場合に特に第1主成分得点が大きくなることがわかります。そしてこの特徴が該当するのは特に中期の作品であるということが言えそうです。
第1主成分得点

第1主成分負荷
続けて第2主成分ですが、これは後期作品がプラス(+)でそれ以外が第6交響曲がややプラスであることを除くと、概ねマイナス(ー)であることがわかります。負荷を確認すると、これは興味深い特徴を持っています。つまり状態遷移パターンのエントロピー、マルコフ過程としてのエントロピーのいずれについても、深さが浅いものがプラスで深くなるにつれてマイナスになっていく傾向があるものが、この成分の得点が高いことになります。これは予備分析において、遷移パターン数と系列長の比について見た時に、後期作品は浅いところから割合が高くなってしまって、深くなっても頭打ちになるのに対して、特に初期作品では浅いところでの割合は低いのに対して、深くなるにつれて系列数が増えていく傾向にあるという点が確認できましたが、それと類似した傾向であると考えられます。であるとすれば、本分析において、この後結果を報告するパターン数/系列長比に基づく分析でも同様の結果がでることが予想されます。更に第2主成分について興味深いのは、マルコフ・エントロピーが小さい程得点が高くなる傾向に対して、後期作品の得点が高くなっていることで、特に移置・転回を考慮しない系列での二重マルコフ・エントロピーと、特に移置・転回を考慮した系列でのマルコフ・エントロピーについて大きなマイナスの負荷を持っている点が注目されます。この点については、最後の考察で取り上げたいと思います。
第2主成分得点
第2主成分負荷
3.2.パターン数/系列長比に基づく分析の結果
エントロピーに基づく分析の結果を踏まえて、パターン数/系列長比に基づく分析の結果について見ていきます。
(A)クラスター分析
まずクラスタ―分析ですが、2つの階層クラスタ―分析の結果について、後期作品がグループ化される点はエントロピーに基づく分析と共通ですが、それ以外の作品のグルーピングについては入れ替わりが見られること、またcomplete法とward法では第1交響曲の枝分かれの位置が異なることから、やや分類が不安定であることが窺えます。それは非階層クラスタ分析の結果についても言えて、後期作品とそれ以外の2つに分割するのが比較的安定しているようです。とはいえ、後期作品以外のグループでは第1交響曲が稍々孤立気味でありつつ、その他の作品についての枝分かれは共通していて、一定の傾向によって並んでいることが想定されますので、その点を主成分分析によって確認してみることにします。
階層クラスタ―分析:complete法
階層クラスタ―分析:ward法
非階層クラスタ―分析:k-means法
クラスタ数はGap統計のシミュレーション結果に基づき決定
第1グループ:第1~8交響曲第2グループ:大地の歌,第9,10交響曲 2 3
symA 0 4:初期(第1~4交響曲)
symB 0 3:中期(第5~7交響曲)
symC 0 1:第8交響曲
symD 3 0:後期(大地の歌、第9,10交響曲)
m1 m2 m3 m4 m5 m6 m7 m8 erde m9 m10
2 2 2 2 2 2 2 2 1 1 1
(B)主成分分析
主成分分析のサマリーを確認すると、第1主成分で3/4、第2主成分が2割を占めて、上位2つだけで累積で約95%に達しています。第3主成分まででほぼ99%となり、残りの寄与は1%を切ることから、第3主成分まで得点や負荷のデータを取りましたが、以下では第1主成分・第2主成分のみについて見ていきます。
PC1 PC2 PC3 PC4 PC5
Standard deviation 3.441 1.8254 0.76159 0.36048 0.25050
Proportion of Variance 0.740 0.2083 0.03625 0.00812 0.00392
Cumulative Proportion 0.740 0.9483 0.98455 0.99267 0.99660
まず2種のプロットを確認すると、左上の象限に後期作品が固まり、原点を挟んで概ね反対側のにその他の作品が広がっている傾向が読み取れます。最も左上には第1交響曲が位置し、次いで第6交響曲が来て、最も右には第4が位置し、その間に第2,第3のグループ、第5,第7,第8のグループが位置しています。主成分毎の軸方向でみた場合には、特に第2主成分については、第1交響曲と第6交響曲が上半分に入っているため、後期作品以外のグループの中でも第2主成分でもって区別することができそうです。
ggbiplotによる第1・2主成分軸でのプロット
第1主成分は、第6交響曲が若干外れているものの、巨視的には時代区分に沿って、後期になればなるほど得点が小さくなるという傾向を持っていると言えそうです。負荷を確認すると全ての成分がマイナスですから、第1主成分については、パターン数/系列長比について見た場合、初期から後期にかけて、その比が増大していく傾向にあることが読み取れます。そしてこれは、予備分析においても確認できた点でした。それでは本分析のエントロピーに基づく分析でも確認でき、予備分析でも確認できたもう一つの傾向、状態遷移パターンの深さ方向に沿った変化はどうなっているのでしょうか?以下に見るように、それは第2主成分に明確に現れていることが確認できます。
第1主成分得点
第1主成分負荷
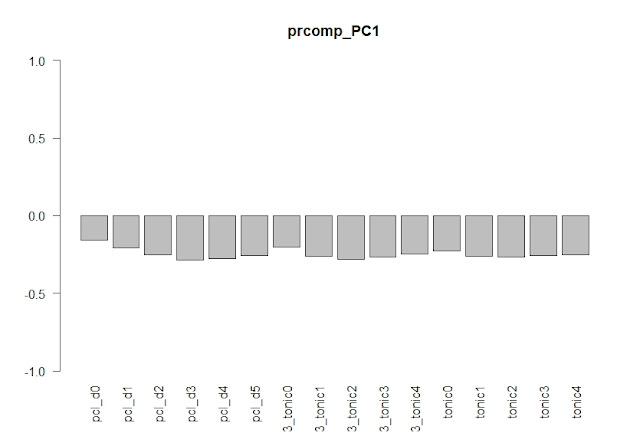
第2主成分得点は、既に二次元プロットで確認した通り、後期3作品以外では、第1、第6交響曲がプラスで、残りの作品はマイナスの得点となっているが、負荷を確認すると、本分析で入力とした3種類の系列抽出条件のそれぞれについて、深さが浅いものの得点が大きく、深さが深いものの得点が小さい程、第二主成分の得点が大きくなるという傾向が鮮明に現れていることが確認できます。従って、予備分析で確認できた傾向および本分析のエントロピーに基づく分析で確認できた傾向は、パターン数/系列長比に基づく分析の結果でも明らかであり、かつそれが、状態遷移パターンの深さに沿ったものであることが明瞭になったように思われます。
第2主成分得点
第2主成分負荷
4.まとめにかえてー予備分析結果との比較ー
- 第1主成分:全般的な多様性(+:多様/-:多様でない)
- 第2主成分:状態遷移の深さと多様性の関係(+:深さに応じて多様性拡大/-:浅いところで既に極限近くまで多様なため、深くなっても多様性が大きくする余地がない)
この傾向は全ての分析において共通していることが今回の分析の結果によって裏付けられています。そしてこの点をマーラーの交響曲について見た時に、以下の点についても、本分析の結果はそれを裏付けるものであると考えられます。その意味では、多様性を手掛かりにした「後期マーラーの挑戦」は本分析でも確認できたように思います。
- 全般的な多様性:後期になると多様性が増大する傾向がある。
- 状態遷移の深さと多様性の関係:後期作品は和音のパターンや浅い状態遷移パターンが多様であり、状態遷移パターンが深くなっても多様性が更に拡大することはないのに対して、その他の交響曲では深くなるのに応じて多様性が拡大する傾向にある。
それでは本分析固有の結果というのは無く、予備分析の結果の確認に留まるのでしょうか?或る意味ではそうであって、予備分析では分析対象とならなかったエントロピーに基づく分析でも、確認できた傾向は同じものであるには違いありません。その一方で、エントロピーに基づく分析結果の中で指摘したこととして、第2主成分においてマルコフ・エントロピーが小さい程得点が高くなる傾向に対して、後期作品の得点が高くなっていることがあります。特に移置・転回を考慮しない系列での二重マルコフ・エントロピーと、特に移置・転回を考慮した系列でのマルコフ・エントロピーについて大きなマイナスの負荷を持っている点が注目されます。これは状態遷移パターンのエントロピーの傾向とは向きが逆であり、パターン数/系列長比の傾向とも逆になっています。この点について実際にエントロピーの計算結果がどうであったかを確認してみると、実際、後期作品のマルコフ・エントロピーは小さいことがわかります。このことはどのように考えればいいでしょうか?
予備分析で確認できたことは、特に後期作品ではパターン数/系列長比が深さが浅いところでも非常に高く、9割を超えていること、そのために深さが深くなっても、それに応じて比が更に高くなることが出来ず、寧ろ頭打ちになる傾向が見られるということでした。そこで極端な場合として、出現する全ての状態遷移パターンが1回しか発生しない場合を考えてみます。このとき状態遷移の系列は、いわば一筆書きとなり、最後に出現するパターンが吸収的状態となるだけでなく、途中の系列も実は確定的であり、状態遷移マトリクスの各行を見た場合に、最後に出現する状態が全ての列において0になる以外、他の全ての行について、ある列の確率が1で他の列は0になっている筈です。更にもう一つ、全ての状態を1回ずつ通って最初に戻り無限に循環するパターンを考えてみると、この状態遷移マトリクスは全ての行である列の確率が1、それ以外の列の確率は0となり、エントロピーの計算結果は0になります(経路が一意に決まっているので、これは当然です)。一方、この場合の状態遷移パターンのエントロピーはある系列長で取りうる最大の値になります。
このようにして出現するパターンは出現しうる極限まで多様になる一方で、状態遷移プロセスは寧ろ確定的になり、ある状態から他の複数の状態に分岐することがなくなっていくことがわかります。またマルコフ過程として見た場合のエントロピーと状態遷移パターンの出現頻度のエントロピーのギャップも明らかになります。そしてこれは人為的な想定ではなく、実際の集計結果を見ても、マーラーの作品の場合、特にその後期作品の場合には、深さが浅い部分でも寧ろこの極限状態に近い状況であることを既に確認しているわけですから、マーラーの後期作品において状態遷移パターンの出現頻度のエントロピーが大きいにも関わらず、マルコフ過程としてのエントロピーが寧ろ小さくなることも説明がつくように思われます。(2023.10.26)
(A)計算の入力データ
サブフォルダ cdnz_tonic_transition
- *_A_cdnz_tonic.csv:各小節頭拍(B)/単音・重音を含む(cdnz)/移置・転回(長短三和音のみ)を区別する(tonic)条件の和音パターン系列を単純マルコフ過程として見た場合の状態遷移マトリクス
サブフォルダ cdnz_tonic_transition2
- *_A_cdnz_tonic.csv:各小節頭拍(B)/単音・重音を含む(cdnz)/移置・転回(長短三和音のみ)を区別する(tonic)条件の和音パターン系列を二重マルコフ過程として見た場合の状態遷移マトリクス
サブフォルダ cdnz_tonic_frq
- *_A_frq_tonic.csv:各小節頭拍(B)/単音・重音を含む(cdnz)/移置・転回(長短三和音のみ)を区別する(tonic)条件の和音パターン系列に出現する和音パターンの出現頻度の集計結果
サブフォルダ cdnz3_tonic_transition
- *_A_cdnz3_tonic.csv:各小節頭拍(B)/単音・重音を含まず(cdnz3)/移置・転回(長短三和音のみ)を区別する(tonic)条件の和音パターン系列を単純マルコフ過程として見た場合の状態遷移マトリクス
サブフォルダ cdnz3_tonic_transition2
- *_A_cdnz3_tonic.csv:各小節頭拍(B)/単音・重音を含まず(cdnz3)/移置・転回(長短三和音のみ)を区別する(tonic)条件の和音パターン系列を二重マルコフ過程として見た場合の状態遷移マトリクス
サブフォルダ cdnz3_tonic_frq
- *_A_frq3_tonic.csv:各小節頭拍(B)/単音・重音を含まず(cdnz3)/移置・転回(長短三和音のみ)を区別する(tonic)条件の和音パターン系列に出現する和音パターンの出現頻度の集計結果
サブフォルダ cdnz3_pcls_transition
- *_A_cdnz_tonic.csv:各小節頭拍(B)/単音・重音を含まず(cdnz3/移置・転回を区別しない(pcl)条件の和音パターン系列を単純マルコフ過程として見た場合の状態遷移マトリクス
サブフォルダ cdnz3_pcls_transition2
- *_A_cdnz3_pcl2.csv:各小節頭拍(B)/単音・重音を含まず(cdnz3/移置・転回を区別しない(pcl)条件の和音パターン系列を二重マルコフ過程として見た場合の状態遷移マトリクス
サブフォルダ cdnz3_pcl_frq
- *_A_frq_tonic.csv:各小節頭拍(B)/単音・重音を含まず(cdnz3/移置・転回を区別しない(pcl)条件の和音パターン系列をに出現する和音パターンの出現頻度の集計結果
(B)計算結果・分析の入力データ
サブフォルダ entropy
- entropy_A_tonic.xlsx:マルコフ過程として見た場合の状態遷移マトリクスに基づくエントロピー計算結果(本分析の入力)
- 各拍(A)/単音・重音は対象外(cdnz3)/移置を区別・転回は長短三和音のみ区別(tonic)。
- 単純マルコフ・エントロピー(markov3_tonic1)
- 二重マルコフ・エントロピー(markov3_tonic2)
- 深さ0~4の状態遷移パターン・エントロピー(frq3_tonic0~4)
- 各拍(A)/単音・重音を含む(cdnz)/移置を区別・転回は長短三和音のみ区別(tonic).。
- 単純マルコフ・エントロピー(markov_tonic1)
- 二重マルコフ・エントロピー(markov_tonic2)
- 深さ0~4の状態遷移パターン・エントロピー(frq_tonic0~4)
- 各拍(A)/単音・重音は対象外(cdnz3)/移置・転回を区別せず(pcl)
- 単純マルコフ・エントロピー(markov3_pcl1)
- 二重マルコフ・エントロピー(markov3_pcl2)
- 深さ0~4の状態遷移パターン・エントロピー(frq_pcl0~5)
サブフォルダ ratio
- ratio_tonic_A.xlsx:和音パターンの出現頻度の集計結果に基づくパターンと系列長の比率の集計結果(本分析の入力)
- 各拍(A)/単音・重音は対象外(cdnz3)/移置を区別・転回は長短三和音のみ区別(tonic)。
- 深さ0~4のパターン数/系列長比(3_tonic0~4)
- 各拍(A)/単音・重音を含む(cdnz)/移置を区別・転回は長短三和音のみ区別(tonic).。
- 深さ0~4のパターン数/系列長比(tonic0~4)
- 各拍(A)/単音・重音は対象外(cdnz3)/移置・転回を区別せず(pcl)
- 深さ0~5のパターン数/系列長比(pcl_d0~5)
(C)分析結果
サブフォルダ ratio_A:エントロピーに基づく分析結果
- 入力データ
- entropy_tonic_A.csv:分析対象の作品毎の和音パターンのエントロピー
- gm_sym_col.csv:対象作品の創作時期に対応した色(主成分得点グラフで使用)
- gm_sym_label.csv:対象作品の作品名ラベル
- 主成分分析結果
- eigen.jpeg:固有値のグラフ
- prcomp_T.jpeg:主成分分析(scale=T)結果のbiplotグラフ
- ggbiplot12.jpeg:主成分分析結果(第1,第2成分)のggbiplotグラフ
- ggbiplot23.jpeg:主成分分析結果(第2,第3成分)のggbiplotグラフ
- pr_score-[1-3]T.jpeg:主成分得点のbarplotグラフ
- prcomp_PC[1-3].jpeg:主成分負荷量のbarplotグラフ
- 階層クラスタ分析結果
- hclust_complete.jpeg:complete法での分類結果
- hclust_wardD2.jpeg:ward法での分類結果
- 非階層クラスタ分析結果
- clusGap.jpeg:ギャップ統計量のシミュレーション結果サンプル
- kmeans3.csv:kmeans法(クラスタ数=3)での分類結果
- kmeans3.jpeg:kmeans法(クラスタ数=3)での分類結果のclusplotグラフ
- 分析履歴
- hist.txt:R言語を用いた分析履歴(Windows版R言語 ver.4.3.1をR studio上で実行)。
- 主成分分析結果サマリを含む。
サブフォルダ ratio_A:パターン/系列長比に基づく分析結果
- 入力データ
- ratio_tonic_A.csv:分析対象の和音パターンの作品毎の出現頻度(深さ0~5)
- gm_sym_col.csv:対象作品の創作時期に対応した色(主成分得点グラフで使用)
- gm_sym_label.csv:対象作品の作品名ラベル
- 主成分分析結果
- eigen.jpeg:固有値のグラフ
- prcomp_T.jpeg:主成分分析(scale=T)結果のbiplotグラフ
- ggbiplot12.jpeg:主成分分析結果(第1,第2成分)のggbiplotグラフ
- ggbiplot23.jpeg:主成分分析結果(第2,第3成分)のggbiplotグラフ
- pr_score-[1-3]T.jpeg:主成分得点のbarplotグラフ
- prcomp_PC[1-3]T.jpeg:主成分負荷量のbarplotグラフ
- 階層クラスタ分析結果
- hclust_complete.jpeg:complete法での分類結果
- hclust_wardD2.jpeg:ward法での分類結果
- 非階層クラスタ分析結果
- clusGap.jpeg:ギャップ統計量のシミュレーション結果サンプル
- kmeans2.csv:kmeans法(クラスタ数=6)での分類結果
- kmeans2.jpeg:kmeans法(クラスタ数=6)での分類結果のclusplotグラフ
- 分析履歴
- hist.txt:R言語を用いた分析履歴(Windows版R言語 ver.4.3.1をR studio上で実行)。 主成分分析結果サマリを含む。
- 共通補助データ
- gm_sym_col.csv:対象作品の創作時期に対応した色(主成分得点グラフで使用)
- gm_sym_label.csv:対象作品の作品名ラベル
[ご利用にあたっての注意] 公開するデータは自由に利用頂いて構いません。あくまでも実験的な試みを公開するものであり、作成者は結果の正しさは保証しません。このデータを用いることによって発生する如何なるトラブルに対しても、作成者は責任を負いません。入力として利用させて頂いたMIDIファイルに起因する間違い、分析プログラムの不具合に起因する間違いなど、各種の間違いが含まれる可能性があることをご了承の上、ご利用ください。