MIDIファイルを入力とした分析：状態遷移パターンの出現確率分布の比較

 1.はじめに

　記事：MIDIファイルを入力とした分析：マルコフ過程としてのエントロピー計算結果（補遺）創作時期別集計において、マーラーの作品を創作時期別に見た場合に、全般的な多様性や状態遷移の深さと多様性の関係において、創作時期によって傾向が変化していく点について、各作品毎ではなく、創作時期別に、更にマーラーの交響曲全体で、単純マルコフ過程として見た場合のエントロピー、深さ0～5の状態遷移パターン出現確率のエントロピー、或いは状態遷移パターン数と系列長の比といった特徴量を集計した結果を報告しました。その結果は、、創作時期によって傾向が変化していくというそれまでの集計・分析に基づく観察と一致するものであったのですが、そこでの比較は数値の単純な比較とそのグラフによる可視化によるもので、定量的に差異を測定した訳ではありません。

　そこで本記事では、マーラーの交響曲全体の状態遷移パターンの出現確率分布と、各作品の状態遷移パターンの出現確率分布との比較を行った結果を報告します。2つの確率分布の比較の方法としては、幾つかの方法が直ちに思い浮かびますが、ここではカルバック・ライブラー・ダイバージェンスと相互情報量の2つを用いました。更に参考として、状態遷移パターンの出現確率のエントロピーについて全体と各作品とを比較した結果も報告します。最後の点は、出現確率分布の比較が、所謂「距離」の定義を満たしているといないとに関わらず（実際にはカルバック・ライブラー・ダイバージェンスは満たしていない訳ですが）、計算して求まる値は両方の差の絶対値であって、非負の量であることから、どちらが多様性がより大きい・小さいといった情報が落ちてしまうのを補うためです。

　更に、カルバック・ライブラー・ダイバージェンスと相互情報量を計算するために用意した状態遷移パターンの出現確率分布を表すベクトル自体を特徴量としてクラスタリングを行ってみましたので、その結果も併せて報告します。なおこれは、以前に行った和音の出現頻度に基づく分類で用いた特徴量と基本的には同じですが、以前の分析では、幾つかの「名前のある」（つまり音楽理論上、機能を持つとされる）和音に対応するパターンに限定して行っていたものを、交響曲全体で出現する全ての和音に対応するパターンを対象として行ったという位置づけになります。直前の記事MIDIファイルを入力とした分析：未分析の和音の出現頻度―エントロピー計算結果の同時代以降の作品との比較の記事撤回についてで取り上げたように、マーラーの作品については未分析の和音はないので、このような分析が可能となっています。

　以下、計算結果に対するコメントはせずに、集計・分析条件の説明と結果の報告のみを行います。また、カルバック・ライブラー・ダイバージェンスと相互情報量の定義などについての説明も割愛させて頂きます。両方とも特に近年の機械学習で用いられていることもあってか、Web上で様々な説明・解説があるようですので、必要に応じてそれらを参照頂けますようお願いします。

2.集計・分析の条件

2.1. カルバック・ライブラー・ダイバージェンスおよび相互情報量の計算

　上掲の創作時期別集計の記事におけるのと同様、単音・重音は対象外(cdnz3)/移置・転回を区別しない(pcl)条件で、今回は各拍(A)毎に抽出した和音パターンの系列のみを対象としました。（A/B系列で大きく見た場合には著しい差異がないと判断し、計算資源の制約に抵触しない限りでは、よりサンプルの多いA系列をもって代表させるのが適当と考えました。）計算対象となる状態は、深さ0（和音＝ピッチクラスの集合のパターン）と深さ1（和音＝ピッチクラスの集合の状態遷移パターン、単純マルコフ過程の状態遷移パターンに相当）です。

　計算にあたっては従来から用いてきたR言語にあるエントロピー計算用のライブラリ(entropy)をRstudio上で使用しました。R言語のバージョンは4.3.1です。entropyライブラリにはカルバック・ライブラー・ダイバージェンスと相互情報量を計算するプラグインが用意されています（それぞれKL.pluginとmi.plugin）ので、それを利用して計算を行いました。既述の通り、特にカルバック・ライブラー・ダイバージェンスは、所謂「距離」の公理を満たしておらず非可換ですが、ここでは個別の作品における確率分布を分子側、交響曲全体における確率分布を分母側として計算を行っています。つまりKLD(P||Q)とした時、P：各曲、Q：全体です。（交響曲全体で出現するパターン（Ｑ側）が個別の作品（P側）で出現しない、つまり確率0であることはありえるが、その逆はないため。逆向きの計算では分母が0になり、値が無限大になってしまいます。）なお、公開した計算結果には交差エントロピーも含めていますが、これは各曲のエントロピーとカルバック・ライブラー・ダイバージェンスから求めることができます。（即ち、H(P, Q) = H(P) ＋ KLD(P||Q)）

　冒頭述べた通り、参考として個別の作品における状態パターンの出現確率のエントロピーと交響曲全体の状態パターンの出現確率のエントロピーとの差分の計算も行いましたが、こちらについては、後者が前者よりも大きければプラス、小さければマイナスの値を取るように計算しました。これは深さ0～5の全てについて計算を行いました。

2.2. 状態遷移パターンの出現確率分布を表すベクトルによるクラスタリング

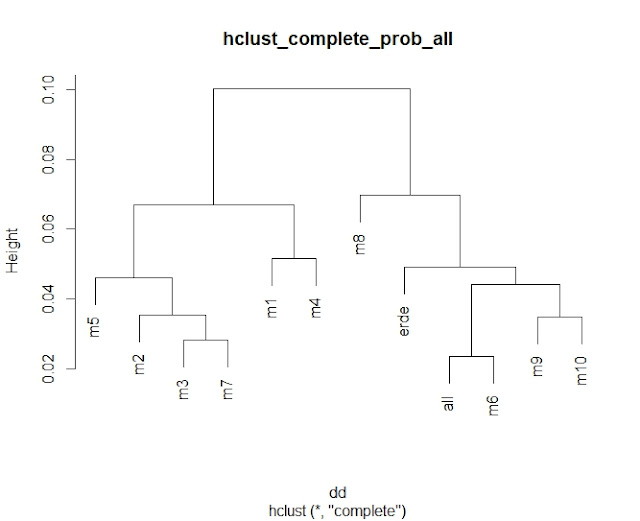
　従来から用いてきたR言語を用い、R言語の階層クラスタリング関数hclustで、complete法により計算を行いました。今回の分析の特徴として、各作品の状態遷移パターンの出現確率分布のベクトル(m1～m10)に加えて、交響曲全体の状態遷移パターンの出現確率分布のベクトル(all)も含めてクラスタリングを行うことで、全体と各作品の距離が視覚的に確認できるようにしてみました。

3.集計・分析結果

3.1.カルバック・ライブラー・ダイバージェンスおよび相互情報量の計算結果（KLD(P||Q)とした時、P：各曲、Q：全体）

(A)深さ＝0

(B)深さ＝1

(参考)出現確率エントロピーの差分（Q－P、但しP：各曲、Q：全体）

※後期作品の深さ0の差分がマイナスになっている点に注意。第8交響曲はわずかにプラスだがほぼ0でした。

3.2. 状態遷移パターンの出現確率分布を表すベクトルによるクラスタリング結果

(A)深さ＝0

(B)深さ＝1

※深さ0と1では、all（全交響曲）とm6（第6交響曲）の位置が異なりますが、後期作品3曲が概ね同じクラスタに属する点では共通しています。

[付録]ダウンロード可能なアーカイブファイルgm_sym_A_KLD_MI_cdnz3_pcl.zip の中には以下のファイルが含まれます。

• 入力ファイル（各交響曲および交響曲全体について）
• gm_A_prob_all.csv：和音パターン出現確率（深さ0）：値のみ
• gm_A_prob2_all.csv：状態遷移パターン出現確率（深さ1）：値のみ
• gm_A_frq_all.csv：和音パターン出現頻度（深さ0）：パターンラベル付き
• gm_A_frq2_all.csv：状態遷移パターン出現頻度（深さ1）：パターンラベル付き
• 結果ファイル（各交響曲および交響曲全体について）
• hist.txt：R言語の実行ログ
• gm_sym_A_KLD_MI_cdnz3R_pcl.xlsx
• 状態（パターン）の出現確率（深さ0～5）
• 対全交響曲の出現確率エントロピー差分（深さ0～5）：（Q－P、但しP：各曲、Q：全体）
• 単純マルコフ過程、二重マルコフ過程としてのエントロピー
• 対全交響曲のカルバック・ライブラー・ダイバージェンス（深さ0,1）：（KLD(P||Q)とした時、P：各曲、Q：全体）
• 対全交響曲の相互情報量（深さ0,1）
• 対全交響曲の交差エントロピー（深さ0,1）

(2023.11.10)

[ご利用にあたっての注意] 公開するデータは自由に利用頂いて構いません。あくまでも実験的な試みを公開するものであり、作成者は結果の正しさは保証しません。このデータを用いることによって発生する如何なるトラブルに対しても、作成者は責任を負いません。入力として利用させて頂いたMIDIファイルに起因する間違い、分析プログラムの不具合に起因する間違いなど、各種の間違いが含まれる可能性があることをご了承の上、ご利用ください。