1.はじめに
記事:MIDIファイルを入力とした分析:状態遷移パターンの出現確率分布の比較では、マーラーの交響曲全体の状態遷移パターンの出現確率分布と、各作品の状態遷移パターンの出現確率分布との比較を行った結果を報告しました。一方、他の作曲家の作品との比較については、マーラーの同時代以降の作品との比較を企て、一旦公開まで漕ぎ着けたものの、未分析の和音が占める割合が高いことに気付き、意味のある集計・分析にならないと判断し、記事を撤回しました。その経緯は記事:MIDIファイルを入力とした分析:未分析の和音の出現頻度―エントロピー計算結果の同時代以降の作品との比較の記事撤回についてに記載した通りです。そして同記事ではマーラーの同時代以降の作品との比較の替わりに、比較対象としてきた他の作曲家の作品における未分析の和音の出現頻度を報告しました。その結果を踏まえ、本記事では、他の作品との比較をしようとした場合に、未分析の和音の割合が比較的小さくて、マーラーの作品に出現する和音および和音の遷移のパターンの範囲に収まり、その頻度の分布の比較をすることが概ね可能な作品を選択して比較を行った結果を報告します。以下、これまでの記事同様、計算結果に対するコメントはせずに、集計・分析条件の説明と結果の報告のみを行います。
但し、これまで本ブログで行ってきた、MIDIファイルを入力としたマーラーの作品の分析を通して見た場合、MIDIファイルから自作のプログラムで抽出した拍毎・小節頭拍毎の和音(ピッチクラスの集合)の連なりを分析しようと試みて、最も初期には和音の系列データそのものを時系列データと見做して、時系列データの比較手法を用いたクラスタリングを検討したものの、和音の系列データの各要素は或る次元を持った量ではなく、ピッチクラスの集合をある規則で符号化して数値化したものであるためにうまく行かず、その後は一定の限定した和音の集合に範囲を限定して、その出現頻度に注目した分析を行ってきたのに対して、状態遷移パターンの出現確率分布を用いて、カルバック・ライブラー・ダイバージェンスのような特徴量を用いた比較を行ったり、出現確率分布のベクトル全体を特徴ベクトルと見做したクラスタリングを行うことによって、漸く和音(ピッチクラスの集合)の系列の全体を表す特徴量を用いた分析が可能になったと言えるのではないかと思います。また、個別の作品間の比較や、それらと他の作曲家の作品との比較に留まらず、マーラーの交響曲全体についての特徴量を計算して、それと個別の作品とを比較することが可能になったこともあって、その一部の次元のみを取り出しているに過ぎないとは言え、漸く「マーラー・オートマトン」の出力の全体を捉えた分析に辿り着いたように感じます。
2.集計・分析の方法
これまでに用いてきた以下の特徴量を集計することとします。各項目それぞれの詳細については各特徴量の集計や分析の結果を報告した過去の記事を参照頂きたく、ここでの説明は割愛させて頂きます。
- 単純マルコフ過程としてみた場合のエントロピー
- 和音パターン・状態遷移パターンの出現確率のエントロピー
- 状態数と系列長の比率
- カルバック・ライブラー・ダイバージェンス
- 相互情報量
- 状態遷移パターンの出現確率分布を表すベクトルによるクラスタリング(階層クラスタ分析:complete法)
このうちカルバック・ライブラー・ダイバージェンスおよび相互情報量については、マーラーの交響曲全曲についての和音パターンおよび状態遷移パターンの出現確率分布を比較対象とした作品のものと比較しますが、比較対象の作品における確率分布を分子側、マーラーの交響曲全体における確率分布を分母側として計算を行うのは、マーラーの各交響曲との比較の場合と同じで、KLD(P||Q)とした時、P:比較対象の作品、Q:マーラーの交響曲全体です。但しマーラーの各交響曲の場合には、交響曲全体で出現するパターン(Q側)が個別の作品(P側)で出現しない、つまり確率0であることはありえるが、その逆はないという条件が成り立ちますが、今回は他の作曲家の作品との比較のため。必ずしも成り立ちません。この時、比較対象の他の作曲家の作品には出現するがマーラーの交響曲には出現しないパターンを含めて出現確率のベクトルを構成すると、計算上、分母が0になり値が無限大になってしまいます。そこでマーラーの全交響曲に出現するパターンのみを対象にして出現確率のベクトルを構成することになりますが、そうすると今度は比較対象の作品に出現するパターンで集計対象にならないパターンが出てきてしまいます。
今回比較対象の候補とした作品は、
記事:MIDIファイルを入力とした分析:未分析の和音の出現頻度―エントロピー計算結果の同時代以降の作品との比較の記事撤回について記載の確認結果を踏まえ、未分析の和音が無いか、あっても極僅かな作品としましたが、その中でも、実際に計算をしてみると、マーラーの交響曲には出現しないパターンを数多く持った作品が出てきてしまいます。また、その割合は当然ですが、和音のパターンについての場合と、状態遷移パターン(ここでは深さ1のみ)についての場合とでは大きく異なります。A、Bという和音が出現しても、A→Bという状態遷移が生じるとは限りませんし、B→Aについても同じことが言えます。従ってある比較対象の作品に出現する和音のパターンが全てマーラーの全交響曲に含まれる場合でも、それら和音の組み合わせである状態遷移パターンについては、その比較対象の作品に出現するパターンがマーラーの全交響曲に出現するとは限りません。そこで本記事の分析にあたっては、そのような未集計のパターンがどれくらい出現するかの集計も同時に行い、結果を報告する対象に含めるかどうかを判断することにしました。
具体的には、マーラーの全交響曲(gm_all)との比較対象とする作品の候補として、以下を選択しました。
- ブルックナー:第5,7,8,9交響曲(ab5,7,8,9)
- ブラームス:第1~4交響曲(jb1,2,3,4)
- シベリウス:第2,7交響曲、「タピオラ」(js2,7, jsTapiola)
- フランク:交響曲、交響的変奏曲、弦楽四重奏曲、ヴァイオリン・ソナタ(cfsym, cfsymvar, cfsq, cfvp)
- ヤナーチェク:シンフォニエッタ(lj)
- タクタキシヴィリ:ピアノ協奏曲第1番(ot)
- ラヴェル:左手のための協奏曲、ピアノ協奏曲、優雅で感傷的な円舞曲、「ダフニスとクロエ」第2組曲(mr1, mr2, mr3, mr4)
これらについて、まず上述のように未集計のパターンののべ数を確認します。まずは単独和音パターン(深さ=0に相当)についての集計結果を示します。
一見して、ラヴェルの作品における未集計和音の数が多いことがわかります。(他の作曲家は全くないか、あっても1曲につき数個。)ラヴェルの作品の系列長は他の作曲家の作品に比べれば相対的に短めですから、系列長の中で占める割合は更に大きいことになります。
同様に、前後の和音の対からなる状態遷移パターン(深さ=1に相当)について、未集計パターンを見ますが、こちらはのべ数そのものではなく、対象となる系列長の中で、未集計のものが占める割合を以下に示します。
こちらでもラヴェルの作品の未集計パターンの割合の多さは明らかです。シベリウスの作品も「タピオラ」はラヴェルの作品と同等の割合であり、第7交響曲も高めですが、ラヴェルにおけるように半分前後の割合に達する作品はありません。また、深さ0の集計結果も併せて考えると、ラヴェルについては系列のうちのかなりの割合が実質的に分析の対象から外れてしまうことになり、結果の意味合いについて留保がつくことになります。
そこで本記事の分析においては、ラヴェルの作品は対象外とすることにしました。一方、同様にして、深さ=2,3,4,5の状態遷移パターンについても集計を行った時にどのような結果になるのかについても確認してみたくなりますが、本稿では深さ0,1に限定し、それ以上の深さについての集計・分析は後日を期することとします。
3.集計・分析結果
3.1.エントロピーおよび多様性の計算結果(比較対象の作品およびマーラーの全交響曲(右端))
(A)単純マルコフ過程として見た場合のエントロピーおよび状態遷移パターンの出現確率のエントロピー(深さ0~5)
(B)パターン数/系列長比(深さ0~5)
3.2.カルバック・ライブラー・ダイバージェンスおよび相互情報量の計算結果(KLD(P||Q)とした時、P:比較対象の作品、Q:マーラーの全交響曲)
(A)深さ=0
(B)深さ=1
(参考)出現確率エントロピーの差分(Q-P、但しP:各曲、Q:全体)
未集計のパターン数が多いシベリウスの第7交響曲、「タピオラ」では深さ0の差分がマイナスになっており、マーラーの全交響曲よりもエントロピーが大きいことが確認できる。
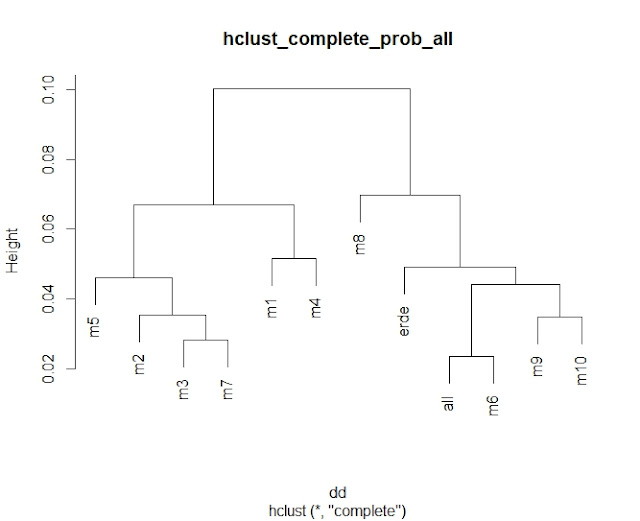
3.3. 状態遷移パターンの出現確率分布を表すベクトルによるクラスタリング結果
(A)深さ=0
(B)深さ=1

- 入力ファイル(比較対象の作品およびマーラーの全交響曲について)
- gm_control_A_prob_all.csv:和音パターン出現確率(深さ0):マーラーの全交響曲の列を含む。ラヴェルの作品は含まず。クラスタ分析の入力。
- gm_control_A_prob2_all.csv:状態遷移パターン出現確率(深さ1):マーラーの全交響曲の列を含む。ラヴェルの作品は含まず。クラスタ分析の入力。
- control_A_prob_all.csv:和音パターン出現確率(深さ0):比較対象作品のみ。ラヴェルの作品は含まず。gm_control_A_prob_all.csvのサブセット。
- control_A_prob2_all.csv:状態遷移パターン出現確率(深さ1):比較対象作品のみ。ラヴェルの作品は含まず。gm_control_A_prob2_all.csvのサブセット。
- *_A_cdnz3_pcl.csv:比較対象の各作品(ラヴェルの作品も含む)の状態遷移パターン出現頻度(深さ0~5)
- *_A_cdnz3_pcl_transition.csv:比較対象の各作品(ラヴェルの作品も含む)の状態遷移マトリクス
- 結果・中間結果ファイル(比較対象の作品およびマーラーの交響曲全体について)
- hclust_complete_prob_all.jpg:状態遷移パターンの出現確率分布を表すベクトルによるクラスタリング結果(深さ=0)
- hclust_complete_prob2_all.jpg:状態遷移パターンの出現確率分布を表すベクトルによるクラスタリング結果(深さ=1)
- control_A_pcl_KLD_MI.xlsx
- Sheet1シート:比較対象の作品およびマーラーの交響曲全体について
- 総拍数
- 状態数(深さ0~5)
- 系列長(深さ0~5)
- パターン数/系列長比(深さ0~5)
- 単純マルコフ過程としてのエントロピー
- 状態(パターン)の出現確率(深さ0~5)のエントロピー
- 対マーラー全交響曲の出現確率エントロピー差分(深さ0~5):(Q-P、但しP:各曲、Q:マーラー全交響曲)
- 対マーラー全交響曲のカルバック・ライブラー・ダイバージェンス(深さ0,1):(KLD(P||Q)とした時、P:各曲、Q:マーラー全交響曲)
- 対マーラー全交響曲の相互情報量(深さ0,1)
- 対マーラー全交響曲の交差エントロピー(深さ0,1)
- 未集計系列数・深さ0:未集計和音パターンののべ数
- 未集計系列数・深さ1:未集計状態遷移パターンののべ数
- 未集計系列比率・深さ1:未集計状態遷移パターンののべ数の系列長に対する割合
- d0シート:和音パターン出現頻度(深さ0):比較対象作品のみ。ラヴェルの作品を含む。
- d0pシート:和音パターン出現確率(深さ0):比較対象作品のみ。ラヴェルの作品を含む。
- d1シート:状態遷移パターン出現頻度(深さ1):比較対象作品のみ。ラヴェルの作品を含む。
- d1pシート:状態遷移パターン出現確率(深さ1):比較対象作品のみ。ラヴェルの作品を含む。
(2023.11.13)
[ご利用にあたっての注意] 公開するデータは自由に利用頂いて構いません。あくまでも実験的な試みを公開するものであり、作成者は結果の正しさは保証しません。このデータを用いることによって発生する如何なるトラブルに対しても、作成者は責任を負いません。入力として利用させて頂いたMIDIファイルに起因する間違い、分析プログラムの不具合に起因する間違いなど、各種の間違いが含まれる可能性があることをご了承の上、ご利用ください。