これまでMIDIファイルを入力とした分析の一環として、和音(コード)の出現頻度に基づくマーラーの交響曲作品50ファイル(楽章単位)の他の作品71ファイルとの比較を試みた結果を「MIDIファイルを入力とした分析:和音の出現頻度から見たマーラー作品」として報告し、次いでその第2報として比較対象となる作品数を増やして、マーラーの作品50ファイルに対して、他の作曲家の作品200ファイルの合計250ファイルでの分析結果について「MIDIファイルを入力とした分析:和音の出現頻度から見たマーラー作品(その2:拡張版)」として報告しました。更に2つの報告を補完する分析として、各和音毎の出現頻度の傾向を、マーラーの交響曲と比較対象となる作品群との間で比較した、「MIDIファイルを入力とした分析:和音の出現頻度から見たマーラー作品(その3:補遺 )」を公開しました。
その後、集計プログラムの制約で、対象作品のMIDIデータの各ファイルに含まれる最初の1591拍分のみが分析対象となっていることが判明したため、ファイルに含まれる全ての拍を対象とした分析を、比較対照用のデータを増やし、合計300ファイルを対象として実施した結果を、「MIDIファイルを入力とした分析:和音の出現頻度から見たマーラー作品(その4:全拍対象・比較対照作品追加・割合比較)」および「MIDIファイルを入力とした分析:和音の出現頻度から見たマーラー作品(その5:全拍対象・比較対照作品追加・傾向分析)」として公開しました。
上記の経緯を踏まえ、この記事では、マーラーと他の作曲家の作品との間の比較ではなく、マーラーの作品間の比較を目的として主成分分析・因子分析・クラスタ分析を実施した結果について示します。
1.対象データ
マーラーの作品のうち、本分析に利用可能なMIDIファイルが公開されている以下の作品。(合計64ファイル、以下の括弧内はファイル数。)
- 「大地の歌」、交響曲第1番~第10番(クック版)計11曲の各楽章(50)
- 「さすらう若者の歌」(4)
- 「リュッケルトによる5つの歌曲」(5)
- 「子供の死の歌」から第1曲「いま太陽は晴れやかに昇る」 (1)
- 「子供の魔法の角笛」から「夏の交替」「魚に説教するパドヴァの聖アントニウス」「ラインの小伝説」「美しいトランペットが鳴り響くところ」(4)
分析は以下の2つの単位で行った。
(1)交響曲楽章50および歌曲14の合計64ファイルについてファイル単位(2)交響曲(第10番クック版、「大地の歌」を含む11曲)について作品単位
2.分析に用いた特徴量
対象データの各拍に出現する和音パターンのうち、抽出対象とした131種のうち、(1)対象作品全体(2)交響曲全体のそれぞれの合計の上位40位まで。3.分析手法
分析はすべてR言語(version 4.1.0 (2021-05-18版)を用いて行った。
分析履歴をアーカイブに含めた。(hist.txt)
A.主成分分析:prcompを使用。
スケーリングについては、(1)ファイル単位の分析ではスケーリングを行わず(scale=FALSE)、説明率89%⇒第7主成分までについて負荷と主成分得点を計算。
(2)交響曲の作品単位の分析では、従来通りスケーリングを行う(scale=TRUE)場合と行わない(scale=FALSE)場合の両方を実施。
前者では説明率93%⇒第7主成分までについて負荷と主成分得点を計算。
後者では説明率91%⇒第4主成分までについて負荷と主成分得点を計算。
分析結果はggbiplotとbiplotでグラフ化。負荷と主成分得点はbarplotでグラフ化。
なおスケーリングについて、ここでコメントをしておきたい。prcompのscale引数は論理値型でデフォルトではF、即ちスケーリングを行わない。スケーリングを行うか行わないかの違いは、分析を行う行列の違いであり、スケーリングを行う場合には相関行列から、スケーリングを行わない場合には、分散共分散行列から主成分分析が行われる。スケーリングを行わないのがデフォルトなのはR言語の仕様の歴史的な事情によるものであり、分析に用いる特徴量が同一単位でありかつ等分散であることが保障されない限りは、通常、スケーリングは実施するものとされている。
今回の分析についていえば、使用している特徴量は全て、ある和音のあるファイルの中での出現頻度であるからスケーリングをする必要はない筈である。(問題になるとしたら寧ろ、特徴量間に相関があることの方であろう。)ところが、従来のマーラー作品と他の作曲家の作品との比較対照においてはスケーリングを行った分析結果を公開してきており、更に今回はファイル単位の分析についてはスケーリングを行わず、交響曲の作品単位での分析ではスケーリングを行う場合と行わない場合の両方の結果を示すことにしたが、これらの方針については異論が考えられるので、ここでの立場を述べておきたい。
今回の分析に限って言えば、スケーリングを行わない場合、ある和音の出現頻度と別の和音の同じファイル・作品での出現頻度の比はそのままに分析が行われるのに対して、スケーリングを行えば、相関行列の計算結果によってその比が調整されるという見方ができるだろう。いずれの場合でも、ある和音の出現頻度のファイル(楽章なり作品)間での違い(2-2-a.の地形図では、横軸方向の高さの比)の傾向は保たれるのだが、和音の間の比(2-2-a.の地形図では奥行方向の高さの比)については、スケーリングを行うことで調整がされ、今回のケースでは、大まかに言って、2-2-b.の出現頻度の降順に並べたグラフで横軸方向に右下がりとなるグラフにおける頻度の下がり具合が小さくなることになる。一例を挙げるならば、スケーリングをしない場合には、長三和音(19)・短三和音(25)がそれぞれ全体の約15%,約8%を占めていて、40位の増四度(65)が約0.5%を占めているので、長三和音/短三和音/増四度の出現頻度比は30/16/1であるのが、スケーリングをすると相関行列の計算結果に基づいて調整がされることにより、この比が小さくなる。その結果として分析における主成分負荷の各特徴量における大きさ(biplotで表示される各和音の負荷量の矢印の長さ)の差が、スケーリングをすることで小さくなっていることが確認できる。結果として各作品のグラフの中での相対的な位置関係のトポロジーについては大まかには保存されているものの、具体的な空間内での方向や距離については変化が起こることになる。言ってみれば、今回のケースにおいてスケーリングを行うことは、各和音間の出現頻度の割合の大小の違いよるバイアスを除いて、それぞれの和音の出現頻度の作品ないし楽章(ファイル)の間での違いについて、異なる単位の特徴量を用いた主成分分析におけるようにスケーリングを行うことによって、恰も和音毎にそれぞれ独立に考慮したらどうなるかを示していることになると考えられるだろう。
一方、上記とは別に、分析に用いる変数(特徴量)よりもサンプルの数が少ない場合の分析の有効性に問題があることが指摘されている。今回の分析では、(2)交響曲の作品単位の分析においてはサンプル数が11であるのに対して、変数である出現頻度割合の和音の数を40としているので、まさにこの問題のケースに該当していることになる。だがこれは、技術的なレベルで捉えた時には、因子分析である手法を採用した場合に相関行列ないし共分散行列がランク落ちして逆行列が求まらないという問題が生じるからであり、実際、今回のケースでも因子分析はそのために実施していない。一方で主成分分析は計算上、上記のような問題とは関係がないため、計算上は支障がない。だからといって計算結果が信頼できるかどうかは別の問題であり、これを回避しようと思えば、変数選択を行い、分析に使用する和音の数を減らせばよいわけであるが、実際に分析をした結果、大きな問題はなさそうであったため、この点については今後、更に分析・検討を行って、より適切な結果に置換していく可能性はあるが、一旦は40変数での結果をそのまま示すこととしたものである。
B.因子分析:factanalを使用。(2)交響曲の作品単位だとサンプル数が11であり、特徴量40に対して少なすぎて分析できないため、(1)ファイル単位の場合のみ実施。
因子数の決定は相関行列の固有値を参照:固有値が2以上⇒5因子と決定。
rotationはvarimax(直交回転), promax(斜交回転)の両方を試行。
分析結果はbilplotでグラフ化。負荷と因子得点はbarplotでグラフ化。
なお作品ないし楽章における和音の出現頻度の割合という同じ特徴量を用いて、主成分分析と因子分析という異なる因果関係を持つ分析を行うことの是非についての考え方を記していおきたい。よく知られているように、主成分分析は多数の観測変数から少数の主成分(合成変数)を作り出す手法であり、観測変数が原因、主成分は結果であるのに対して、因子分析は観測変数に影響を与えている共通因子を抽出する方法であり、共通因子が原因で観測変数が結果となることから、両分析では因果関係が逆になるとされる。ここで観測変数は和音の出現頻度割合であるから、主成分分析では出現頻度割合によって和音がどのようにグルーピングできるかを示しており、因子分析では複数の和音の出現頻度割合に影響を与えている共通因子を仮定して、それぞれの共通因子が、どの和音の出現頻度割合にどれくらい寄与しているのかを示していることになる。従って、一般には、ある対象に対して分析を行い際には、どちらの分析を行うのが妥当であるかを検討すべきであると言われることが多いのだが、ここでの立場は、和音の出現頻度割合について、予めて特定の因果関係を前提とせずに、観点の違う分析を行って、結果を眺めることでマーラーの作品間の特徴の違いを探ることを目的としている。ちなみに因子分析においては変数がサンプル数よりも多い場合に問題が起こる場合があることが知られており、今回も実際に、交響曲について作品単位(サンプル数11)で40種類の和音の出現頻度割合を用いて因子分析を行おうとすると、相関行列のランク落ちが発生して、事前共通性の推定値に用いる重相関係数の2乗(SMC)が求めることができないため、作品単位の分析には因子分析は用いていない。同様の状況で主成分分析を行うことの是非については、主成分分析について記載した部分でコメントをしているので、そちらを参照されたい。
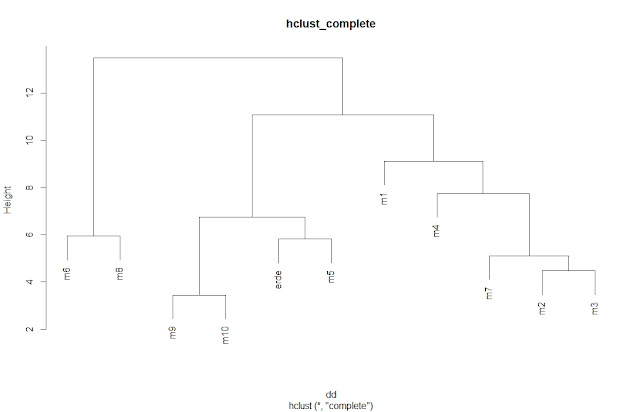
C.階層クラスタリング:hclustを使用。(1)(2)の両方で実施。
いずれもcomplete(デフォルト)、average、ward02の3種類の方式で計算。
結果をデンドログラムでグラフ化。
4.分析結果の概要
以下では分析結果の概要を示すことを目的とし、結果の一部のみを示す。詳細については後述のアーカイブファイル中の結果を参照。
(1)ファイル単位の分析結果の概要
A.主成分分析
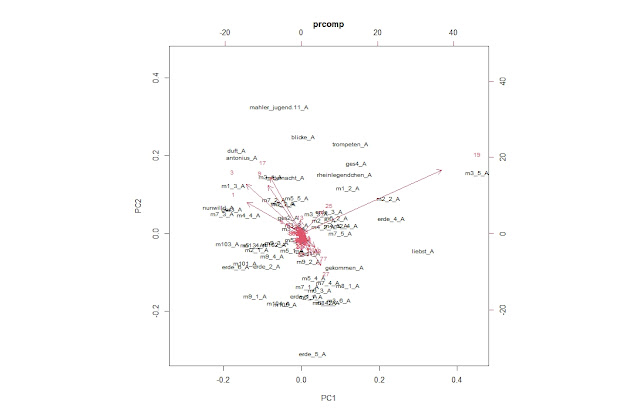
A-1-1.第1、第2主成分でプロット
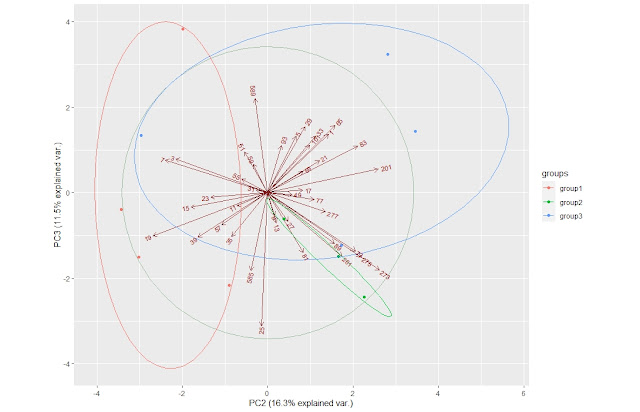
A-1-2.作曲時期別に色分けをした結果:初期(第1~4)交響曲(赤)・中期(第5~7)交響曲(緑)・後期(第8~10と大地の歌)交響曲(水色)
A-1-3.作品別に色分けをした結果A-a.主成分分析(スケーリングあり)
A-a-1-1.第1、第2主成分でプロット
A-b.主成分分析(スケーリングなし)
A-b-1-1.第1、第2主成分でプロット
A-b-1-2.第1、第2主成分でプロット:作曲時期で色分けした結果
初期(第1~4)交響曲(赤)・中期(第5~7)交響曲(緑)・後期(第8~10と大地の歌)交響曲(水色)





















0 件のコメント:
コメントを投稿